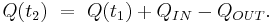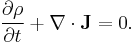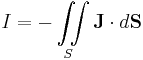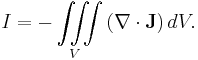Charge conservation

In physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved. The principle was first discovered by American scientist and statesman Benjamin Franklin around 1747.

In practice, charge conservation is a physical law that states that the net change in the amount of electric charge in any volume of space is exactly equal to the net amount of charge flowing into the volume minus the amount of charge flowing out of the volume. In essence, charge conservation is an accounting relationship between the amount of charge in a region and the flow of charge into and out of that same region.

Mathematically, we can state the law as a continuity equation:

Q(t_2) \ = \ Q(t_1) + Q_{IN} - Q_{OUT}.

Q(t) is the quantity of electric charge in a specific volume at time t, QIN is the amount of charge flowing into the volume between time t1 and t2, and QOUT is the amount of charge flowing out of the volume during the same time period.

This does not mean that individual positive and negative charges cannot be destroyed. Electric charge is carried by subatomic particles such as electrons and protons, which can be created and destroyed. In particle physics, charge conservation means that in elementary particle reactions that create charged particles, equal numbers of positive and negative particles are always created, keeping the net amount of charge unchanged. Similarly, when particles are destroyed, equal numbers of positive and negative charges are destroyed.

Although conservation of charge requires that the total quantity of charge in the universe is constant, it leaves open the question of what that quantity is. Most evidence indicates that the total charge in the universe is zero; that is, there are equal quantities of positive and negative charge.

Contents

Formal statement of the law

Vector calculus can be used to express the law in terms of charge density ρ (in coulombs per cubic meter) and electric current density J (in amperes per square meter):

\frac{\partial \rho} {\partial t} + \nabla \cdot \mathbf{J} = 0.

This statement is equivalent to a conservation of four-current. In the mid-nineteenth century, James Clerk Maxwell postulated the existence of electromagnetic waves as a result of his discovery that Ampère's law (in its original form) was inconsistent with the conservation of charge. After correctly reformulating Ampère's law, Maxwell also realized that such waves would travel at the speed of light, and that light itself must be a form of electromagnetic radiation. See electromagnetic wave equation for a full discussion of these discoveries.

Mathematical derivation

The net current into a volume is

I=- \iint\limits_S\mathbf{J}\cdot d\mathbf{S}

where S = ∂V is the boundary of V oriented by outward-pointing normals, and dS is shorthand for NdS, the outward pointing normal of the boundary ∂V. Here \mathbf{J} is the current density (charge per unit area per unit time) at the surface of the volume. The vector points in the direction of the current flow.

From the Divergence theorem this can be written

I=- \iiint\limits_V\left(\nabla\cdot\mathbf{J}\right)dV.

Charge conservation requires that the net current into a volume must necessarily equal the net change in charge within the volume.

\frac{dq} {dt} =- \iiint\limits_V\left(\nabla\cdot\mathbf{J}\right)dV.

Charge is related to charge density by the relation

q = \iiint\limits_V \rho dV.

This yields

0 = \iiint\limits_V \left( \frac{\partial \rho} {\partial t} + \nabla \cdot \mathbf{J} \right)dV.

Since this is true for every volume, we have in general

\frac{\partial \rho} {\partial t} + \nabla \cdot \mathbf{J} = 0.

Connection to gauge invariance

Charge conservation can also be understood as a consequence of symmetry through Noether's theorem, a central result in theoretical physics that asserts that each conservation law is associated with a symmetry of the underlying physics. The symmetry that is associated with charge conservation is the global gauge invariance of the electromagnetic field.[1] This is related to the fact that the electric and magnetic fields are not changed by different choices of the value representing the zero point of electrostatic potential 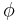\phi \,. However the full symmetry is more complicated, and also involves the vector potential 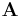\mathbf{A}\,. The full statement of gauge invariance is that the physics of an electromagnetic field are unchanged when the scalar and vector potential are shifted by the gradient of an arbitrary scalar field \chi \,:

\phi' = \phi - \frac {\partial \chi}{\partial t} \qquad \qquad \mathbf{A}' = \mathbf{A} + \nabla \chi. \,

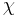In quantum mechanics the scalar field is equivalent to a phase shift in the wavefunction of the charged particle:

\psi' = e^{i\chi}\psi\,

so gauge invariance is equivalent to the well known fact that changes in the phase of a wavefunction are unobservable, and only changes in the magnitude of the wavefunction result in changes to the probability function 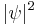|\psi|^2 \,. This is the ultimate reason for charge conservation.

Gauge invariance is a very important, well established property of the electromagnetic field and has many testable consequences. The theoretical justification for charge conservation is greatly strengthened by being linked to this symmetry. For example gauge invariance also requires that the photon be massless, so the well-established lack of mass of the photon could be regarded as a confirmation that charge is conserved.

See also

Notes

  1. ↑ Bettini, Alessandro (2008). Introduction to Elementary Particle Physics. UK: Cambridge University Press. pp. 164–165. ISBN 0521880211. http://books.google.com/books?id=HNcQ_EiuTxcC&pg=PA164&lpg=PA164&sig=luNaWBSntSRav1k9W7_ZhwsDe54.